Deep Learning Notes - Week 1

NLP入门计划第一周 - 笔记

内容

1. 了解感知机/多层感知机(MLP)
2. 了解前向传播，反向传播，微积分， 偏导的基本知识
3. 梯度下降，学习率，梯度裁剪
4. 了解常用的激活函数，从$tanh$到$gelu$
5. 了解loss function, cross-entropy, 平方差

笔记

由于之前有过一点深度学习基础，不算是完全从零开始学起，此次做笔记的目的在于加深对深度学习基础知识的了解，特别是补了一下一些数学上的理论知识。经验浅薄，有所疏漏在所难免。

感知机(Perceptron)

感知机用于线性可分数据的二分类任务，基本思想是通过求解能够划分两类数据的直线或者超平面以达到分类的目的。

按照《统计学习方法》一书的介绍，下面从模型，策略，算法三块来介绍。

1. 模型

   感知机可以表示为如下形式:

   $$f(x) = sign(wx + b)$$

   即一个空间上的超平面。其中$w$为该超平面的斜率，$b$为该超平面的截距。

   最终学习的目标就是学习到一个能够把数据点分到该朝平面两侧的超平面。

2. 学习策略

   • 误分类点：

     误分类点即被超平面错误分类的点，其$f(x)$值和实际的标签$y$恰好相反

     误分类点可以提供修正模型的数据

   • 损失函数：

     即误分类点到超平面的总距离，最终的目标就是让该值尽可能小

     损失函数表示如下：

     $$-\dfrac{1}{\|w\|}\displaystyle\sum_{x_i\in M}|w\cdot{x_i}+{b}|$$

3. 训练算法

   随机梯度下降

   思想：随机初始化超平面，每次随机选择一个误分类点使超平面梯度下降，不断重复，直到所有点被正确分类或者损失函数达到一个阈值（如果是线性不可分的数据是不可能求出能正确分类的超平面的）

多层感知机(multilayer perceptron)

$多层感知机(MLP) = 人工神经网络(ANN)$

单层感知机只能处理线性可分的数据，因此遇到更复杂的数据时，感知机就没有作用了。

多层感知机的结构如下图所示（这里使用了一张别人博客中的图片，点击此处跳转到博客原文）：

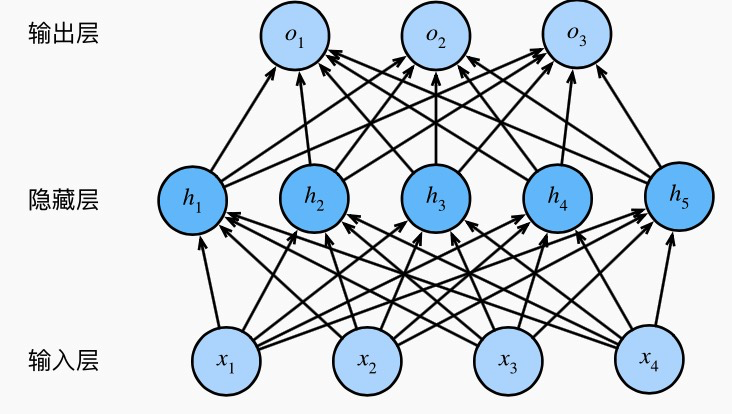
如上图所示，多层感知机其实就是一个全连接的神经网络。上图所示为一个含一层隐含层的网络。这里的$h_1 = w_1x + b$实际上就是一个感知机，多个感知机层叠到一起，构成了一个多层感知机。

但是，如果隐藏层的单元$h_1, h_2, …, h_n$如果直接输入到下一层，那么该多层感知机实际上仍然只能处理线性可能的数据，也即是说，仍然等价于一个单层的感知机，只不过参数更多更复杂而已。要使其能够处理非线性可分的数据，必须加入激活函数（引入非线性），这时隐含层的单元值有所变化，下面以$h_1$为例：

$$h_1 = sigmoid(w_1x + b)$$

这样的网络，才是一个真正的多层感知机。

前向传播(forward propagation)

如前节，按照图中的描述，输入层数据$X$经过计算可以得到隐含层数据$H$，再由隐含层数据经过计算得到输出层的数据$O$，这样一个过程，就是前向传播。

反向传播(backpropagation)

模型的训练过程即是求解目标函数最优值的过程。（目标函数即是代价函数，用于衡量训练结果和实际标签的差异）

反向传播即是通过梯度下降方法，从最后一层开始，使用每一层的梯度值逐层更新每一层的参数值，最终不断逼近最优解（可能是局部最优）

学习率

每次更新的幅度大小，$0 <= lr <= 1$

梯度消失和梯度爆炸

当函数的偏导值接近0，会出现梯度消失（即该参数无法通过梯度进行更新）。梯度消失和激活函数的选取以及网络结构有关。

梯度爆炸的原因暂时还未理解，后续补坑。

梯度裁剪

可以防止梯度爆炸问题发生

激活函数

常用激活函数及其导数

1. sigmoid
   • 原函数 $$sigmoid(x)=\dfrac{1}{1+e^{-x}}$$
   • 导数 $$sigmoid(x)^{'}=sigmoid(x)(1-sigmoid(x))$$
2. tanh
   • 原函数 $$tanh(x)=\dfrac{e^x-e^{-x}}{e^x+e^{-x}}=2sigmoid(2x)-1$$
   • 导数 $$tanh(x)^{'}=1-tanh(x)^2$$
3. ReLU(线性整流单元)
   • 原函数 $$f(x)=\begin{cases}x &\text{if } x\ge0 \\ 0 &\text{if }x<0\end{cases}$$
   • 导数 $$f(x){'}=\begin{cases}1 &\text{if } x\ge0 \\ 0 &\text{if }x<0\end{cases}$$
4. leakly ReLU
   • 原函数 $$f(x)=\begin{cases}x &\text{if } x\ge0 \\ \alpha{x} &\text{if }x<0\end{cases}\left(\alpha=0.1\right)$$
   • 导数 $$f(x){'}=\begin{cases}1 &\text{if } x\ge0 \\ \alpha &\text{if }x<0\end{cases}(\alpha=0.1)$$
5. ELU (SELU)
   • 原函数 $$f(x)=\begin{cases}x &\text{if } x\ge0 \\ \alpha\left({e^x-1}\right) &\text{if }x<0\end{cases}\left(\alpha=0.1\right)$$
   • 导数 $$f(x){'}=\begin{cases}1 &\text{if } x\ge0 \\ \alpha{e^x} &\text{if }x<0\end{cases}(\alpha=0.1)$$
6. GELU
   • 原函数 $$f(x)=0.5x(1+tanh(\sqrt{\dfrac{2}{\pi}}(x+0.44715x^3)))$$
   • 导数
7. softmax
   • 原函数 $$f(x)=\dfrac{e^{Z_j}}{\sum_{k=1}^{K}{e^{Z_k}}}$$
   • 导数
8. Maxout
   • 原函数 $$f(x)=max(W_1x+b_1, W_2x+b_2)$$
   • 导数

损失函数

损失函数是$f(X)$和$Y$的非负实值函数——《统计学习方法》

• 0-1 损失 $$L(f(X),Y)=\begin{cases}1,&Y\not=f(X)\\0, &Y=f(X)\end{cases}$$
• 平方损失 $$L(f(X),Y)=(Y-f(X))^2$$
• 绝对损失 $$L(f(X),Y)=|Y-f(x)|$$
• 对数损失 $$L(Y,P(Y|X))=-\log{P(Y|X)}$$
• 均方误差 $$MSE=\dfrac{1}{n}(\sum{\hat{y_i}-y_i})^2$$

交叉熵

用于衡量预测的概率分布和实际概率分布的差异

$$Cross-Entropy=-\sum_{i=1}^np(x_i)\log(q(x_i))$$